JDAsim
Dokumentation
Beschreibung der integrierten Funktionen
und Operatoren
Modellelemente
Durch einen Doppelklick auf die Fragezeichenflächen der Objekte
kann das Modellgleichungseigenschaftenfenster aufgerufen werden.
Modellgleichungseditor
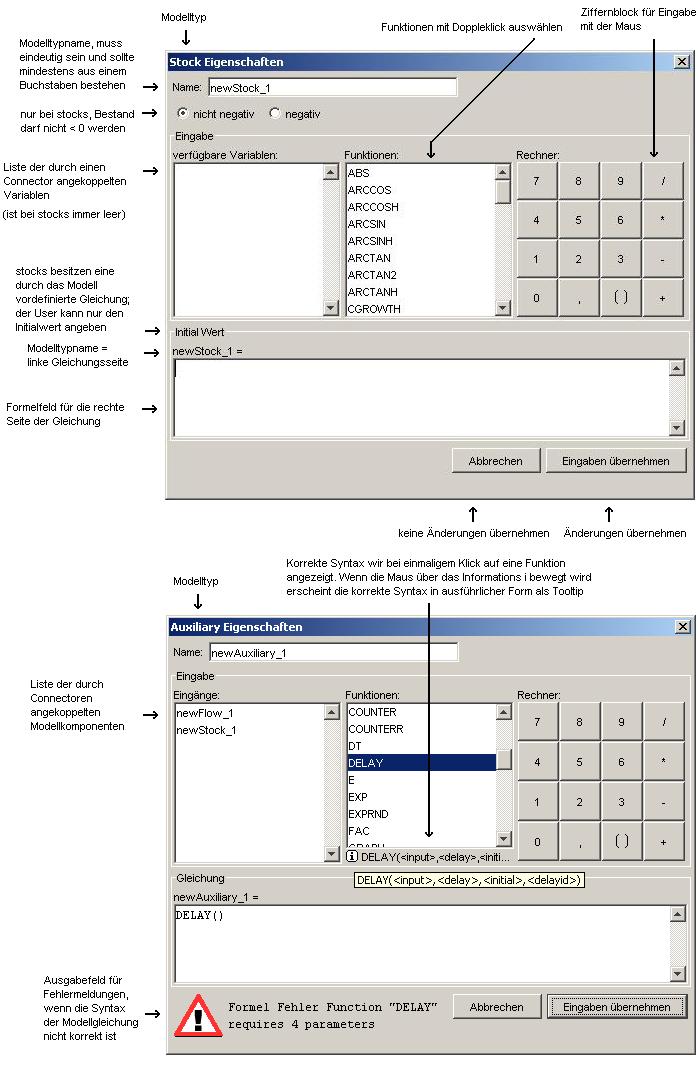
Funktionen
Durch einen Doppelklick auf die Fragezeichenflächen der Objekte
kann das Modellgleichungseigenschaftenfenster aufgerufen werden.
ABS(<expression>)
Mit ABS() kann man sich von einer bestimmten Zahl den Absolutwert
(=positiver Wert)
zurückgeben lassen.
ARCCOS(<expression>)
Mit ARCCOS() kann man sich den Arcuscosinus-Wert zu <expression> im Bogenmaß
zurückgeben lassen. Der Wert <expression> sollte zwischen -1.0 und 1.0
liegen.
ARCCOSH(<expression>)
Mit ARCCOSH() kann man sich den hyperbolischen Arcuscosinus-Wert
zu <expression> im Bogenmaß
zurückgeben lassen.
ARCSIN(<expression>)
Mit ARCSIN() kann man sich den Arcussinus-Wert zu <expression> im Bogenmaß
zurückgeben lassen. Der Wert <expression> sollte zwischen -1.0 und 1.0
liegen.
ARCSINH(<expression>)
Mit ARCSINH() kann man sich den hyperbolischen Arcussinus-Wert
zu <expression> im Bogenmaß
zurückgeben lassen.
ARCTAN(<expression>)
Mit ARCTAN() kann man sich den Arcustangens-Wert zu <expression> im Bogenmaß
zurückgeben lassen.
ARCTAN2(<expression>,
<expression>)
Mit ARCTAN2() kann man sich den Arcustangens-Wert der Parameter x und y
zurückgeben lassen. Dabei wird das Vorzeichen beider Parameter
ausgewertet und so der Quadrant des Ergebnisses bestimmt. Entspricht
den Polarkoordinaten (r, theta).
ARCTANH(<expression>)
Mit ARCTANH() kann man sich den hyperbolischen Arcustangens-Wert
zu <expression> im Bogenmaß
zurückgeben lassen.
CGROWTH(<percentage>)
Diese Funktion wird oftmals eingesetzt, um einen Stock um einen
bestimmten Prozentsatz <percentage> pro Zeiteinheit wachsen zu
lassen. Das Wachstum ist dabei unabhängig von der verwendeten
Simulationsschrittweite dt.
COS(<radians>)
Mit COS() kann man sich den Cosinus-Wert im Radianten
zurückgeben lassen.
COSH(<expression>)
Mit COSH() kann man sich den hyperbolischen Cosinus-Wert im
Radianten zurückgeben lassen.
COUNTER(<start>,<end>)
Eine Zählfunktion, die in Bezug auf logische Funktionen oder sich
wiederholende lineare Funktionen verwendet werden kann. Die Funktion
beginnt mit dem Inkrementieren immer zum Simulationszeitpunkt 0. Die
Inkrementierungsschrittweite ist dabei von der Simulationsschrittweite
dt abhängig. Der <start>-Wert enthält den
Anfangszählwert und der <end>-Wert den Zielwert. Nachdem der
Zielwert erreicht wurde, beginnt die Funktion erneut vom
<start>-Wert aus zu inkrementieren.
COUNTERR(<start>,<end>,<initialvalue>)
COUNTERR ist eine Mischung aus der Zählfunktion COUNTER, der
RAMP-Funktion und der STEP-Funktion, mit dem Unterschied, dass es sich
dabei um keine sich wiederholende Funktion wie bei der COUNTER-Funktion
handelt. Der Wert <start> gibt in diesem Fall den Startzeitpunkt
und der Wert <end> den Endzeitpunkt der Funktion an. Die Funktion
beginnt mit dem Inkrementieren immer zum Simulationszeitpunkt
<start> und addiert den aktuellen Inkrementierungswert zu dem mit
<initialvalue> spezifizierten Wert. Die
Inkrementierungsschrittweite ist dabei von der Simulationsschrittweite
dt abhängig. Hat die Funktion den Endzeitpunkt <end>
erreicht, gibt sie erneut, genau wie vor dem Startzeitpunkt
<start>, den Wert 0 zurück.
DELAY(<input>,<delay>,<initial>,<delayid>)
DELAY gibt den um die Zeit <delay> verzögerten
<input> zurück. Bis <delay> abgelaufen ist, wird der
<initial>-Wert zurückgegeben. Jeder DELAY muss eine
eindeutige <delayid> besitzen. Zur Berechnung der
Verzögerung werden stets die aktuelle Simulationszeit und die
Simulationsdauer benötigt. Diese Funktion ist wichtig für
Größen, die erst nach einer bestimmten Verzögerung
wirksam werden. Dies ist z.B. die Inkubationszeit bei einer Epidemie.
DT
Gibt die Simulationsschrittweite dt zurück, die in den
Simulationsparametern festgelegt wurde
E
Gibt die Eulerscher Zahl e zurück (e = 2.7183...).
EXP(<expression>)
Mit exp() wird die Eulerscher Zahl e mit der übergebenen Zahl <expression> potenziert. Dabei ist die
Eulerscher Zahl e=2.7183.
EXPRND(<lambda>,<seed>)
Mit EXPRND() erhält man exponentialverteilte Zufallszahlen mit
lambda als Mittelwert und einem seed als eindeutige ID. Ein
seed verändert den Zustand eines Zufallszahlengenerators so,
dass stets
die gleiche Folge von Zufallszahlen, abhängig vom Wert des seed
(long
value), erzeugt wird. Dadurch können die Ergebnisse aus
verschiedenen
Simulationsläufen besser miteinander verglichen werden. Die
exponential Verteilung wird oftmal benutzt um eine konstanten
Fehlerrate zu simulieren
FAC(<positive integer>)
Gibt die Fakultät für eine positive ganze Zahl zurück
GRAPH(<double>,<double>,<double>,<double>,...,<input>)
Viele Simulationsaufgaben lassen sich nur mit nichtlinearen Funktionen
realisieren. Die GRAPH-Funktion ist ein mächtiges Mittel, um
eigene, abschnittsweise definierte Funktionen in das
Simulationsprogramm einzufügen. Dabei entsprechen die Parameter
<double, double> jeweils Koordinatenpaaren der Form <x,y>.
Es können beliebig viele davon eingegeben werden. Sie müssen
in Bezug auf die Reihenfolge der x-Werte dabei in aufsteigender Form
geordnet sein. Das bedeutet, die Funktion
GRAPH(<x1>,<y1>,<x2>,<y2>,...,<input>)
muss entsprechend x1 < x2 < xn geordnet sein. Die Eingabefunktion
input sollte sich variabel verhalten, um das gewünschte Mapping
durchführen zu können. Es werden mindestens 5 Parameter
benötigt. Der erste Parameter muss immer der 0-Punkt der gedachten
x-Achse sein.
IF (<logicalexpression>,
<returniftrue>, <returniffalse>)
Die IF() Funktion überprüft die logische Bedingung
<logicalexpression> und
gibt <returniftrue>, wenn die logische Bedingung
wahr ist, und <returniffalse>, wenn sie falsch ist,
zurück.
LOG10(<expression>)
Mit LOG10() kann man sich den Logarithmus (Logarithmus zur Basis 10)
des Parameters <expression> zurückgeben lassen.
LOGN(<expression>)
Mit LOGN() kann man sich den natürlichen Logarithmus (zur Basis
e=2.7183 - Eulerscher Zahl) des Parameters <expression> zurückgeben lassen.
MAX(<expression>,<expression>,...)
Mit MAX() kann man sich den größten Wert der
übergebenen Argumente (1 bis n) zurückgeben
lassen.
MEAN(<expression>,<expression>,...)
Berechnet das arithmetische Mittel aus den Argumenten 1 bis n
MIN(<expression>,<expression>,...)
Mit MIN() kann man sich den kleinsten Wert der übergebenen
Argumente (1 bis n) zurückgeben lassen.
MOD(<expression>,<modulus>)
Berechnet den Modulus Wert zu einer <expression>
NORMAL(<mean>,<std>,<seed>)
Mit NORMAL() erhält man normalverteilte Zufallszahlen mit mean =
Mittelwert, std = Standardabweichung und seed = eindeutige ID. Ein seed
verändert den Zustand eines Zufallszahlengenerators so, dass
stets die gleiche Folge von Zufallszahlen, abhängig vom Wert des
seed (long value), erzeugt wird. Dadurch können die Ergebnisse aus
verschiedenen Simulationsläufen besser miteinander verglichen
werden.
PCT(<fraction>)
Gibt eine Zahl als Pozentsatz zurück. 0.1 --> 10%
PI
Mit PI kann man sich den Näherungswert der Kreiszahl Pi
zurückgeben lassen. Dieser kann dann z.B. für
Kreisberechnungen genutzt werden.
POISSON(<mu>,<seed>)
Mit POISSON() erhält man normalverteilte Zufallszahlen
mit mu = Mittelwert und einem seed als eindeutige ID. Ein
seed verändert den Zustand eines Zufallszahlengenerators so,
dass stets
die gleiche Folge von Zufallszahlen, abhängig vom Wert des seed
(long
value), erzeugt wird. Dadurch können die Ergebnisse aus
verschiedenen
Simulationsläufen besser miteinander verglichen werden. Die
POISSON Verteilung wird verwendet um die Anzahl von Ereignissen in
einem gegebenen Zeitintervall zu modellieren.
PULSE(<volume>,<first
pulse>,<interval>)
Die PULSE-Funktion generiert in rhythmischen Intervallen
<interval> Impulse der Höhe <volume>. Der
Startzeitpunkt wird dabei durch <first pulse> festgelegt. Die
Höhe kann auch eine Variable sein, so dass variabel hohe Impulse
erzeugt werden. Diese Funktion kann zur Untersuchung des
Schwingungsverhaltens von Systemen verwendet werden.
RAMP(<slope>,<time>)
Mit dieser Funktion kann man den verzögerten Einsatz einer
linearen Funktion modellieren. Der Wert der Funktion ist gleich 0 bis
zum Zeitpunkt <time>, danach steigt der Wert mit jedem
Simulationsschritt dt mit der Steigung <slope> kontinuierlich
linear an.
RANDOM(<min>,<max>,<seed>)
Mit RANDOM() erhält man gleichverteilte Zufallszahlen mit min, max
als Intervallgrenzen und einem seed als eindeutige ID. Ein
seed verändert den Zustand eines Zufallszahlengenerators so,
dass stets
die gleiche Folge von Zufallszahlen, abhängig vom Wert des seed
(long
value), erzeugt wird. Dadurch können die Ergebnisse aus
verschiedenen
Simulationsläufen besser miteinander verglichen werden. Wenn keine
Intervallgrenzen und nur der seed angegeben werden, erhält man
gleichverteilte Zufallszahlen zwischen 0 und 1.
ROUND(<expression>,<roc>)
Mit ROUND() wird eine Zahl <expression> auf- oder abgerundet.
Mit <roc> kann man die Nachkommastellen angeben, nach denen
gerundet wird. Zulässige Werte sind 1,10,100,1000,10000 bis
10^n
SIN(<radians>)
Mit SIN() kann man sich den Sinuswert im Radianten zurückgeben
lassen.
SINH(<expression>)
Mit SINH() kann man sich den hyperbolischen Sinuswert im Radianten
zurückgeben lassen.
SQRT(<expression>)
Mit SQRT() kann man sich die Quadratwurzel des Wertes <expression> zurückgeben lassen.
STEP(<height>,<time>)
Die STEP-Funktion verhält sich ähnlich wie die
PULSE-Funktion, mit dem Unterschied, dass die Höhe <height>
zu einem bestimmten Zeitpunkt <time> erreicht wird und ab diesem
Zeitpunkt beibehalten wird. Vor diesem Zeitpunkt gibt die Funktion
immer den Wert 0 zurück.
SUM(<expression>,<expression>,...)
Mit SUM() können die Argumente 1 bis n aufsummiert werden.
TAN(<radians>)
Mit TAN() kann man sich den Tangenswert im Radianten zurückgeben
lassen.
TANH(<expression>)
Mit TANH() kann man sich den hyperbolischen Tangenswert im
Radianten zurückgeben lassen.
TIME()
Mit TIME() kann man sich die aktuelle Simulationszeit
zurückgeben lassen
Operatoren
|
Operatorname
|
|
Operator
|
|
Power
|
|
^
|
|
Boolean Not
|
|
!
|
|
Unary Plus, Unary Minus
|
|
+x, -x
|
|
Modulus
|
|
%
|
|
Division
|
|
/
|
|
Multiplication
|
|
*
|
|
Addition, Subtraction
|
|
+, -
|
|
Less or Equal, More or Equal
|
|
<=, >=
|
|
Less Than, Greater Than
|
|
<, >
|
|
Not Equal, Equal
|
|
!=, ==
|
|
Boolean And
|
|
&&
|
|
Boolean Or
|
|
||
|


